Problem

Given an unsorted array, find the maximum difference between the successive elements in its sorted form.

Constraints

All elements in the array are non-negative integers and fit in the 32-bit signed integer range.

Solution

On first look one can notice that it is easy to solve this problem in O(nlogn) time by first sorting the array and finding maximum difference between consecutive numbers.

Now think about if you were asked to solve this in O(n) time, where n is length of array

Now the problem isn’t trivial anymore. We will have to think beyond sorting as any sorting algorithm in the worst case has O(nlogn) complexity.

Let’s look at our first observation:

Observation 1: if mx and mn are the largest and smallest numbers in the array then all numbers of array will lie in the range [mn, mx]

This is a simple enough observation.

Let’s see how we can use this. Consider the following diagram where we represent the numbers on a number line in increasing order:

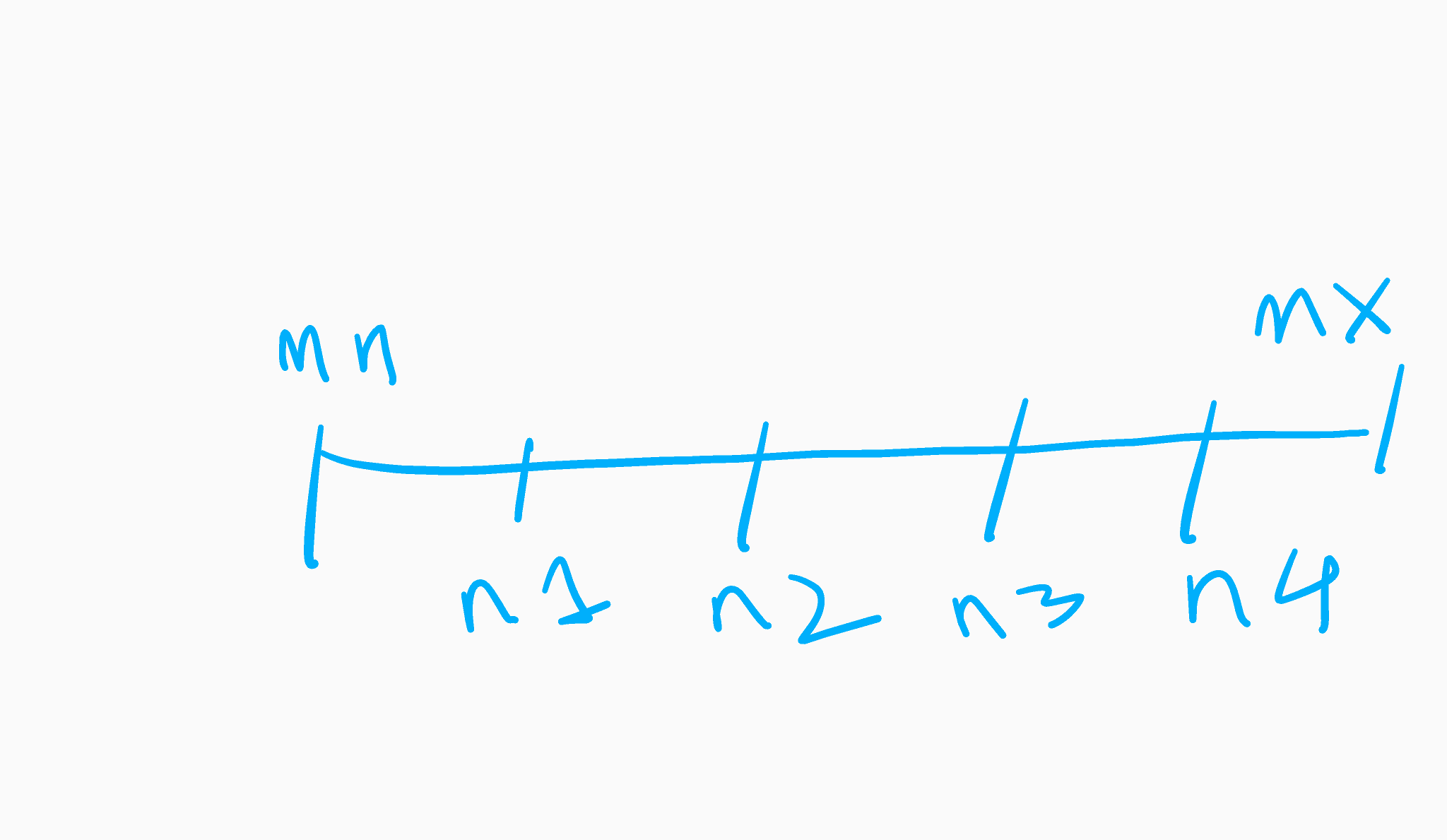
Let N be length of given array. If we ignore mn and mx then we have N-2 numbers. We will distribute these N-2 numbers into some intervals.

Observation 2: If we divide the number line into N-1 equal size intervals then there will be atleast one interval which will be empty.

Proof: Even if we distribute each of the N-2 numbers such that each interval has one number in it then we will have one interval which is empty. If you want some intuition behind it you can read about Pigeonhole Principle.

A thing to notice is that N-1 is only a lower bound on the number of intervals. Any number greator than this will achieve same result.

Let’s see this through an example:

Let, N=5 and arr = [5, 10, 15, 25, 30]

interval_size = ceil((mx - mn) / (N-1)) interval_size = 7

The number line would look something like this:

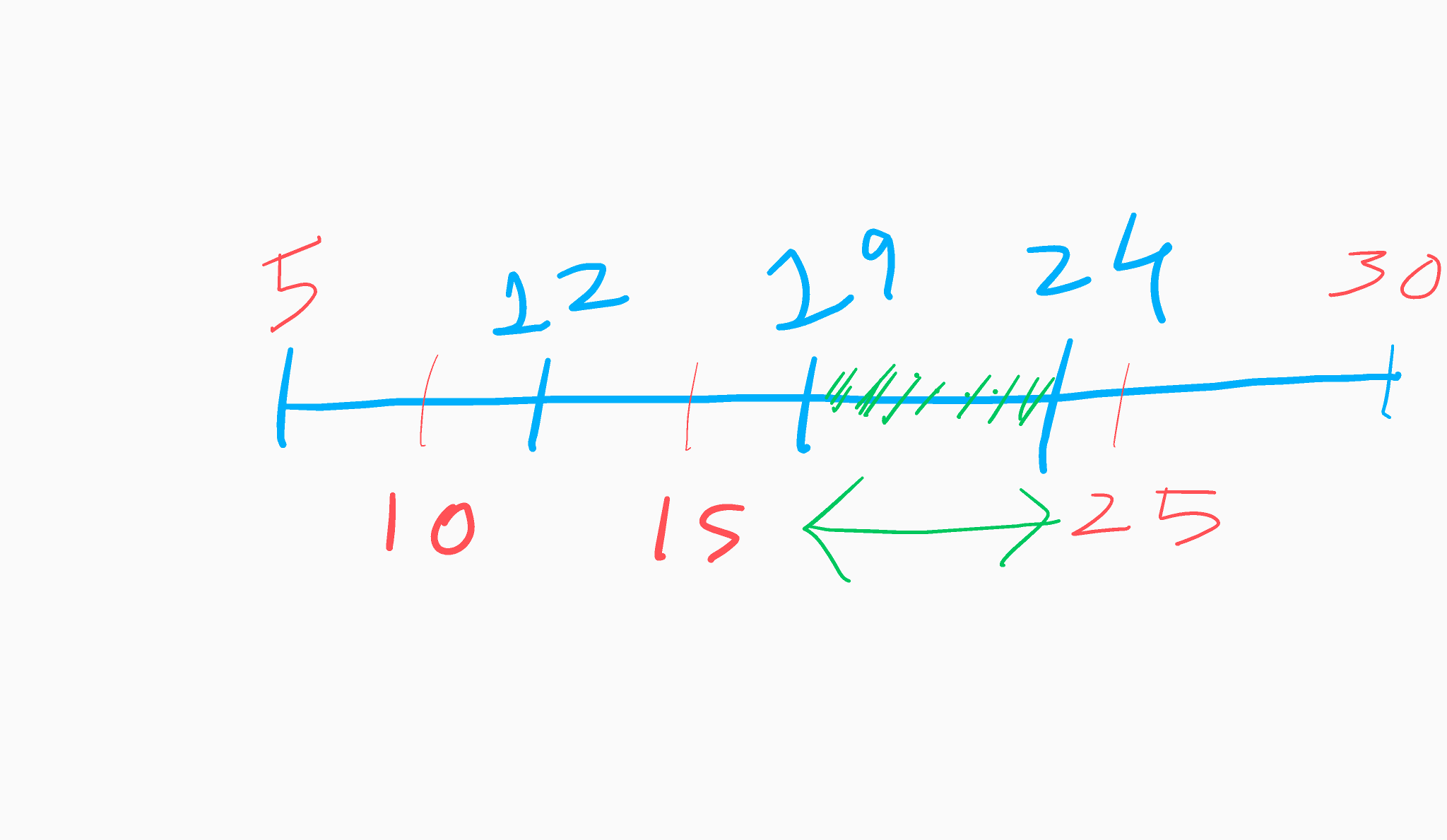
You can see that interval [19, 24) is empty.
So why are we doing this? This leads to our next observation:

Observation 3: For calculating maximum difference between two numbers we can ignore difference between numbers within same interval.

Since we are maximising the difference and are sure that we have at least one empty interval, maximum difference will always be greater than or equal to the interval size.

Therefore, if we know the maximum and minimum of each interval then answer can be updated with: minimum of current interval - maximum of some previous interval. We do this by iterating over each interval from left to right.

Each interval can be represented by tuple of length 3, (a, b, c) where a and b are the minimum and maximum of this interval and c is the count of numbers of this interval.

Time complexity

Since number of intervals is of order O(N) and each interval can be updated in constant time, time complexity of this algorithm is: O(N)

If you want to test your code you can head over to this Link Maximum Gap.

For Implementation see Below: –

class Solution:
    def maximumGap(self, nums: List[int]) -> int:
        if not nums:
            return 0
        mx = max(nums)
        mn = min(nums)
        l = len(nums)
        # ceil ((mx - mn) / l)
        interval_size = (mx - mn + l - 1) // l
        # [a, b, c] where a, b are minimum and maximum of this intervals. c is the count of numbers in this interval.
        intervals = [[inf, -inf, 0] for _ in range(l)]
        for i in range(l):
            if nums[i] == mn or nums[i] == mx:
                continue
            # Find position of interval for current number
            interval = (nums[i] - mn) // interval_size
            # Update minimum and maximum of interval
            intervals[interval][0] = min(intervals[interval][0], nums[i])
            intervals[interval][1] = max(intervals[interval][1], nums[i])
            intervals[interval][2] +=1
        mxsf = mn
        ans = 0
        for i in range(l):
            if intervals[i][2] > 0:
                # ans = max(ans, minimum of current interval - maximum of some previous interval)
                ans = max(ans, intervals[i][0] - mxsf)
                mxsf = intervals[i][1]
        ans = max(ans, mx - mxsf)
        return ans