This is a reiteration of the official Editorial supported with code. Link to Problem -Combination Lock. I would suggest you to read the original problem statement first before going through this editorial.

Problem

Your are given an array of numbers of length W and an integer N. Each number of array, let’s say Wi is in range 1 <= Wi <= N. In one move you can select any number from the array and increase/decrease that number by 1, wrapping around between 1 and N. For example, let’s N=6, and we choose 6. If we increase it should wrap around to 1. Similarly, if 1 is decreased, it becomes 6.

You need to find the minimum number of moves to make all elements of array equal.

Constraints

1 <= W <= 102
2 <= N <= 109

A Brute Force Solution

Observation 1: The moves performed at any index/position in the array is independent of moves performed at any other position.

If we choose a target value T and we want each element to be equal to T, then the moves we perform at any position in array won’t affect moves performed at other positions. Thus, the number of moves at every position can be calculated separately. There are N possible values of T i.e 1 <= T <= N.

Observation 2: There are two possible ‘number of moves’ for a value X to reach T. If T >= X, they are: T - X and N - (T - X). If X >= T then X - T and N - (X - T).

Using above two observation we can construct the brute force solution as

• For each value of T, 1 <= T <= N
  • Calculate number of moves for each position separately and add all of them. Number of moves at each position should be minimum of the two possible values (Observation 2).
• Find minimum of the total moves for all values of T.

Time complexity of this approach is: O(N * W). We are performing W operations for each value of N.
Unfortunately, this is not sufficient to pass the given constraints.
Continue, if you have properly understood the brute force solution.

Improvement of the brute force solution

Observation 3: A major observation is that we can get the minimum possible moves by bringing all the array values to one of the initial values of the array.

Proof

First let’s sort the array. Now, consider a value val that is not equal to any of the initial values of array and we want val to be the target value. Also, consider two numbers from the initial array: Xi and Xj such that Xi is the last number smaller than val and Xj is the first number larger than val.

To optimally reach val each number from initial array has to first reach Xi or Xj. After performing those operations, let n1 numbers are at Xi and n2 numbers are at Xj. Then the final number of moves for all numbers to reach val would be equal to:
(val - Xi) _ n1 + (Xj - val) _ n2.
We can show that this can always be improved by shifting val to either Xi or Xj

1. If n1 < n2 then we can shift val to Xj and the number of operations would become (val - Xi) _ n1 + (Xj - val) _ n1. We are transforming numbers at Xi to value Xj. The numbers at Xj are already at correct place so no operations for them. Similarly,
2. If n2 <= n1 then we can shift val to Xi and the number of operations would become (val - Xi) _ n2 + (Xj - val) _ n2

If you compare then in both cases we have lesser number operations than keeping val unchanged.

The Optimal Solution

So, now we know that the target value is one of the intial values of the array.

Remember that the array is sorted.

Observation 4: Consider, one of the initial values as target value T and two numbers X1 and X2 such that X1 < X2 <= T. Then, it is never possible that X1 reaches T by performing increment operations only and X2 reaches T by performing decrement operations only. If the optimal way for X1 to reach T is by perfoming increment operations then X2 would also prefer increasing as it closer to T than X1.

So, from this we can also conclude that -

1. There exists some position i, 0 <= i <= t such that for all j, 0 <= j < i values at position j prefer decreasing and for all k, i <= k <= t would prefer increasing.
2. There exists some position u, t <= u < W such that for all v, t <= v <= u values at position v prefer decreasing and for all w, u < w < W would prefer increasing.

t is the index of T. We can binary search for i and u for every t we choose.
Let’s see how to find i for certain t. u can be found similarly.

Consider the following scenerio. We know that i is in range [0, t]. Consider mid point of this range let’s say x.

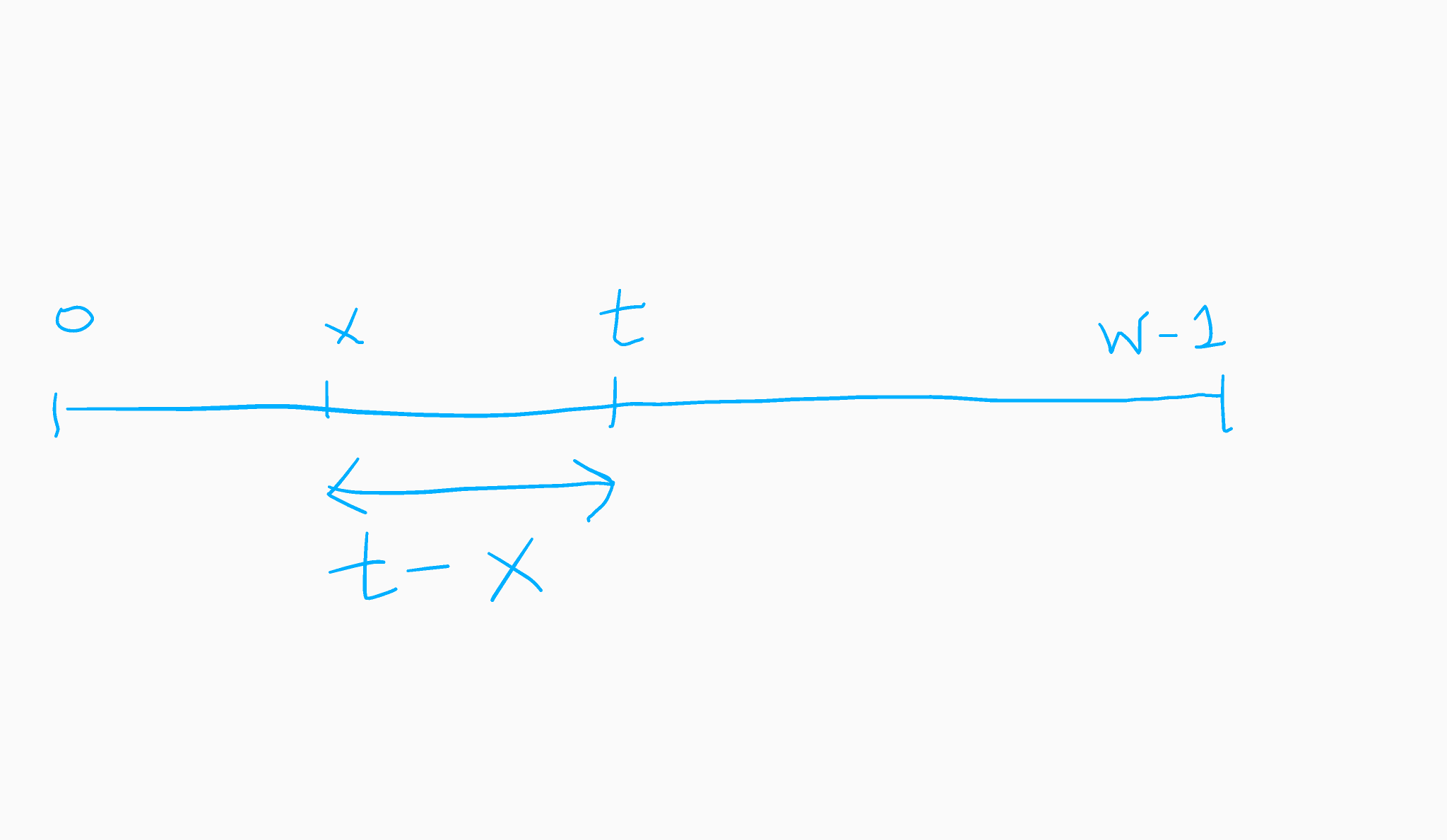
If, T-arr[x] > N - (T-arr[x]) this means that value at x will increase to reach T. This also means that all positions greater than x would also prefer increasing.
So, from this we can say that either i = x or i < x and we can omit the range [x, t]. We have omitted exactly half of the range which is the essence behind Binary Search. We proceed similarly with the other half until i is found. (See code for implementation details)

Now, let’s calculate total moves once we know i and u.
Let’s also assume that we have a function getSum(m, n) which returns arr[m] + arr[m+1] … arr[n] i.e sum of all numbers from postion m to n (inclusive). Extending on the above points we have

1. For range, 0 <= j < i, we have, (Recall Observation 2)

   sum1 = (N - T + arr[i-1]) + (N - T + arr[i-2]) ...
   
   sum1 = i * (N - T) + (arr[i-1] + arr[i-2] .. + arr[0])
   
   sum1 = i * (N - T) + getSum(0, i-1)
   

2. For i <= k <= t,

   sum2 = (T - arr[i]) + (T - arr[i+1]) ..
   
   sum2 = T * (t - i + 1) - getSum(i, t)
   

Similarly, 3. For t <= v <= u, sum3 = getSum(t, u) - (u - t + 1) * T

4. For u < w < W, sum4 = (N + T) * (W - u - 1) - getSum(u+1, W-1)

Thus the total moves for target value T at position t denoted by sum is,
sum = sum1 + sum2 + sum3 + sum4

Also, getSum(m, n) = prefixSum[n] - prefixSum[m-1]
where, prefix[x] is the sum of elements with index less than equal to x. We can preprocess and store prefix[x] to achive a constant time operation to calculate sum.

So, we calculate sum for all possible initial values and take minimum of them which is the answer.

Time complexity of this solution is: O(W * log W)

For implemention see below -

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;


int w, n;
vector<ll> prefix;

ll getSum(int l, int r){
	if (l <= r){
		if (l <= 0) return prefix[r];
		return prefix[r] - prefix[l-1];
	}
	return 0;
}

int main(){
	int t, tc = 0;
	cin >> t;
	while (t--){
		tc ++;
		cin >> w >> n;
		vector<ll> arr(w);
		for (int i=0; i<w; i++)
			cin >> arr[i];
		sort(arr.begin(), arr.end());
		prefix = vector<ll>(w, 0);
		prefix[0] = arr[0];
		for (int i=1; i<w; i++){
			prefix[i] = prefix[i-1] + arr[i];
		}

		ll res = LLONG_MAX;
		for (int i=0; i<w; i++){
			ll op1, op2;
			int p, q;

			int lo = 0, hi = i;
			while (lo <= hi){
				int mid = lo + (hi - lo) / 2;
				op1 = arr[i] - arr[mid];
				op2 = n - op1;
				if (op1 <= op2){
					p = mid;
					hi = mid - 1;
				}
				else{
					lo = mid + 1;
				}
			}

			lo = i, hi = w - 1;
			while(lo <= hi){
				int mid = lo + (hi - lo) / 2;
				op1 = arr[mid] - arr[i];
				op2 = n - op1;
				if (op1 <= op2){
					q = mid;
					lo = mid + 1;
				}
				else{
					hi = mid - 1;
				}
			}
			ll sm1 = 0, sm2 = 0, ans = 0;
			sm1 = (i - p + 1) * arr[i] - getSum(p, i);
			sm2 = p * (n - arr[i]) + getSum(0, p-1);
			ans += sm1 + sm2;

			sm1 = 0, sm2 = 0;
			sm1 = getSum(i, q) - (q - i + 1) * arr[i];
			sm2 = (n + arr[i]) * (w - q - 1) - getSum(q+1, w-1);
			ans += sm1 + sm2;
			res = min(res, ans);
		}
		cout << "Case #" << tc << ": " << res << endl;
	}
}